こんにちは!ドミです!(#^^#)
全国の吹奏楽部が競う吹奏楽コンクール。
吹奏楽部員なら「全国大会に行きやすい自由曲はあるのだろうか?」と一度は考えたことがあると思います。
今回はそんな疑問にお答えするため、過去10年分のコンクールの結果から、全国大会に出場しやすい自由曲を調査しました。
せっかくコンクールに出るなら全国大会に出やすい曲を選びたいですよね。
次回のコンクールの自由曲はコレで決まりだぁ!!
早く結論を知りたい人はこちらからご覧ください。 「全国大会に行きやすい曲」と判断された6曲へ飛ぶ
高校の部はこちらからどうぞ。
吹奏楽コンクールとは

吹奏楽コンクールは「全日本吹奏楽連盟」が主催するコンクールで、吹奏楽の中では最も規模が大きく、 今年で第69回を迎える歴史ある大会です。
各校12分の持ち時間で課題曲と自由曲の2曲を演奏し、その技術力と表現力を競います。
吹奏楽コンクールにおいて全国大会に出場することは全吹奏楽部員のあこがれであり、いわば野球部の甲子園、陸上部のインターハイ、ラグビー部の花園的な存在です。
そんな憧れの全国大会は非常に狭き門で、中学、高校ともに30校ずつしか参加することはできません。
今日も吹奏楽部員は全国大会への出場を目指して練習に励んでいることでしょう。
コンクールでは自由曲の選曲が超重要

吹奏楽コンクールでは課題曲と自由曲の2つの曲を演奏します。
課題曲は毎年4~5曲が事前に運営により決められていて、各校その中から1曲を選びます。
課題曲は4~5種類しかないので、当然他の学校とかぶることが多く、一定レベル以上になると課題曲で差を付けることは難しいです。
そこで重要になってくるのが、自由曲の存在です。
自由曲はその名の通り、各校が自由に選ぶことができる曲です。技術力や表現力を最大限にアピールできる自由曲を選んだ方がコンクールではいい成績を残しやすいということです。
瞬足の「コーナーで差を付けろ!」じゃないですけど、「自由曲で差を付けろ!」という精神がコンクールでは大切ということですね。
全国大会に行きやすい曲の調査

吹奏楽コンクールで全国大会に出場するには、自由曲の選曲が大切です。
となると当然「全国大会に行きやすい自由曲ってあるんだろうか?」という疑問がわきますよね。
吹奏楽部員なら誰しもが一度は考えたことありますよね??
ということで、今回は「全国大会に行きやすい自由曲」について過去のコンクールの結果から調査することとしました。
過去の吹奏楽コンクールの結果は有志によりデータベース化されおり、誰でも簡単に確認できるようになっています。
今回はこちらのデータをありがたく使わせていただき、大人げないほどに、がっつり統計的な分析を行っていきます。
全国大会で最も演奏された曲

全国大会に行きやすい自由曲とはどんなものか?と考えたとき、最初に思いついたのは『全国大会で多く演奏されている自由曲は全国大会に行きやすいと言えるんじゃないか』というものでした。
ということで全68回の全国大会の結果をまとめるぞぉ~と息巻いたのですが、よく考えてみると10年以上前の学生と今の学生では練習環境が大きく異なります。
10年以上前はまだ「ブラック部活」とかいう概念や言葉すらなく、文字通り365日練習している学校もありました。

私の中学校がまさにそれで、本当に365日毎日楽器を吹いてました。当時は当たり前でしたが今の感性では考えられませんね。(;^ω^)
さらに、60年以上前から存在している曲と、最近作曲された曲でも回数に差が出てしまいそうです。
ということで、直近10年分に限ってデータを集めました。
調査の結果(全国の演奏回数)
調査の結果『ウインドオーケストラのためのマインドスケープ (高昌帥) 』が全国出演回数が10回で最も多い結果となりました。
| 順位 | 曲名(作曲者) | 演奏回数 |
| 1 | ウインドオーケストラのためのマインドスケープ (高昌帥) | 10 |
| 2 | 復興 (保科洋) | 8 |
| 2 | 吹奏楽のための風景詩《陽が昇るとき》 (高昌帥) | 8 |
| 2 | ブリュッセル・レクイエム (アッペルモント) | 8 |
| 3 | 大いなる約束の大地~チンギス・ハーン (鈴木英史) | 7 |
- 直近10年分についてのみ調査。
- 対象は全国大会の中学の部
この結果を見て、「そうかぁ、『マインドスケープ』を演奏すればいいのかぁ」と思っていたのですが、、、
よく考えたら全国でたくさん演奏されていても、その裏で大量に落選していたら意味ないです。
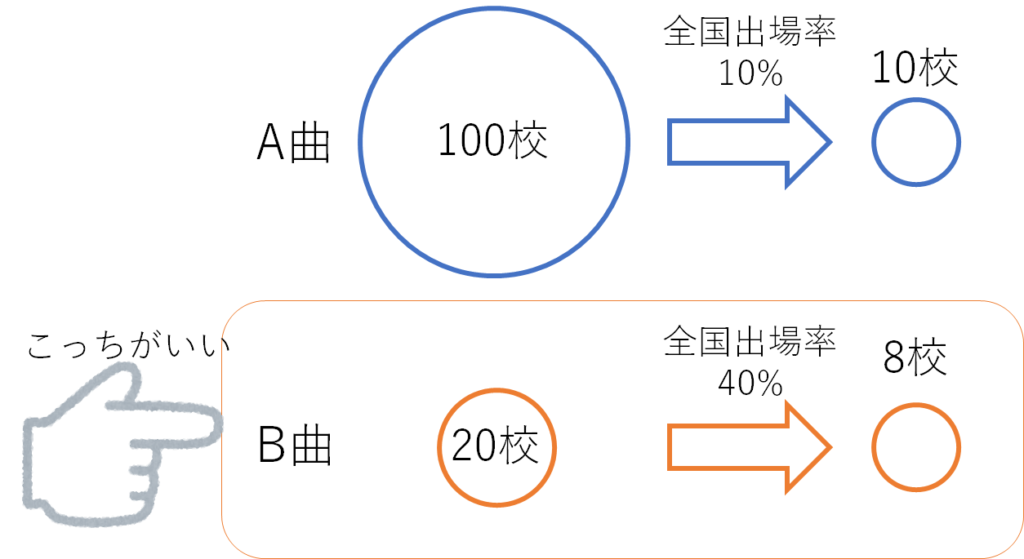
『A』という自由曲を100校が演奏して10校が全国大会に行った場合と、『B』という自由曲を20校が演奏して8校が全国大会に行った場合では『B』の方が「全国大会に行きやすい自由曲」にふさわしいと思います。
ということで自由曲別の全国大会への出場率について追加で調査を行いました。
全国大会の出場率が高い曲

全国大会の出場率を計算する際に注意しないといけないのは各学校の演奏スキルの差です。
選んだ自由曲の影響で全国に行ったor行かなかったというよりも、技術力の差で全国大会に行っている可能性が大きい場合があります。
自由曲毎の全国への出場率を計算するには、技術力が同じくらいの学校のデータでそろえる必要があるのです。
私の経験上、全国大会の一つ手前である支部大会で金賞をとるような演奏はほとんど同じレベルで上手です。金賞の中からどこが全国に行くのか、発表まで分かりません。
ということで、支部大会で金賞を取ったもの同士を比較すれば、技術力的には同じと言っていいでしょう。
データの数があまりに少ないとたまたま全国大会に出場しているだけかもしれないので、10回以上金賞を受賞している曲に絞って分析しました。
調査の結果(全国大会の出場率)
調査の結果、『ウインドオーケストラのためのマインドスケープ (高昌帥) 』は出場率45.5%で第2位でした。
最も出場率が高いのは 『 ブリュッセル・レクイエム (アッペルモント) 』で、その出場率は66.7%ということが分かりました。
| 順位 | 曲名(作曲者(編曲者)) | 金賞回数 | 代表回数 | 全国大会の出場率 |
| 1 | ブリュッセル・レクイエム (アッペルモント) | 12 | 8 | 66.7% |
| 2 | ウインドオーケストラのためのマインドスケープ (高昌帥) | 22 | 10 | 45.5% |
| 3 | 吹奏楽のための風景詩《陽が昇るとき》 (高昌帥) | 19 | 8 | 42.1% |
| 4 | 復興 (保科洋) | 20 | 8 | 40.0% |
| 5 | 歌劇《トゥーランドット》 (プッチーニ (後藤洋)) | 16 | 6 | 37.5% |
- 期間は直近10年分(2010~2019年度)
- すべての支部大会の中学の部を対象
- 支部大会で10回以上金賞を受賞した自由曲のみを対象
この結果を見たときに、「やっぱり『マインドスケープ』は全国でたくさん演奏されているし、出場率も全体で2番目に高いから全国大会に行きやすい曲なんだな」と思いました。
が、
さらによく考えてみると、そもそも金賞を取った時点で全国大会に選ばれる確率は結構高いです。
支部大会で金賞を受賞するのは5~10校ほどあり、その中から2~3校程度が代表に選ばれます。
仮に金賞を10校が受賞し、代表が3校選ばれる場合、完全にランダムに代表が選ばれるとしても全国出場率は10分の3、つまり33.3%程あるのです。
33.3%の確率に対して『マインドスケープ』の全国出場率45.5%は本当に高いと言えるのでしょうか?

さいころを振ると出目が偏る場合があるように、今回『マインドスケープ』を演奏した22校がたまたま高めの確率で全国大会に出場できただけかもしれません。
ということで、次は『マインドスケープ』の出場率45.5%は本当に「高い出場率」と言ってよいのか、統計を使って分析を行いました。
いよいよ統計的分析の本番です。
『マインドスケープ』は全国大会に行きやすい曲と言えるのか

統計的にデータを扱う場合、データの数が多いに越したことはないので、最も金賞受賞の回数が多い『マインドスケープ』の全国出場率について分析しました。
『マインドスケープ』の全国出場率が統計的に高いかどうかを判断するには、「検定」を使用します。
検定とは、ある仮説に基づいて確率を計算し、実際のデータと突き合せたときに、もとの仮説が正しいかどうかを判断するというものです。
例えばあるコインに細工がしてあるかどうか調べる場合。
最初に「このコインは普通のコインで、裏表は2分の1の確率で決まる」と仮定します。
次に、実際にそのコインを10回投げた結果すべて表が出たとしましょう。元の仮説が正しければ今回の実験結果は1028分の1(0.1%)くらいでしか起きない現象です。
この場合、たまたま0.1%のことが起きたというよりは、「表裏の確率が2分の1ではなく、表が出やすいコインだった」と考える方が自然です。
なので、もともとの仮説であった 「このコインは普通のコインで、裏表は2分の1の確率で決まる」 が間違っていたとし、「このコインは表が出やすいように細工がしてあるコインだ」と判断します。

このように、仮説に基づいて実際に起きた事象がどのくらいの確率で起きるのかを計算し、その確率があまりにも低い場合に元の仮説を棄却して判断します。
この一連の流れを「検定」といいます。
ここでは「支部大会で金賞を受賞した学校は自由曲に関係なく、完全にランダムで全国大会の代表に選ばれる」という仮説を立てます。
次に、その仮説をもとにして『マインドスケープ』を演奏した学校が全国大会に行く確率を計算します。
確率を計算した結果、実際に起きた「22校中10校以上の学校が全国に出場する」という現象が上位5%でしか生じない珍しい現象である場合、そんなことはめったに起きないのだから仮説が間違っていたと判断します。
「全国出場に自由曲は関係ない」という仮説が棄却されるため、『マインドスケープ』は「全国大会に行きやすい自由曲」であると言うことができるのです。
ちなみに、上位5%の現象が起きた場合は仮説との差を確認できたという意味から「有意差あり」、上位5%の現象が起きず、仮説が間違っていたと判断できない場合は「有意差なし」と表現します。
また、今回の5%のように、仮説が間違っていたかどうか判断する線引きの確率を「有意水準」といい、αで表します。
- 期間は直近10年分(2010~2019年度)
- すべての支部大会の中学の部を対象(中学のみを対象)
- 支部大会で『マインドスケープ』を演奏し金賞を受賞した学校がある大会のみを対象
- 「金賞を受賞した団体はすべて同じ確率で全国大会に行ける」という仮説を考える
- 仮説が正しいとしたときに、10回以上全国大会に出場できる確率が上位5%以下(α=5%)の場合、仮説を棄却し、『マインドスケープ』は統計的に「全国大会に行きやすい自由曲」と判断する。
自由曲が関係ないときに『マインドスケープ』が全国大会に行ける確率
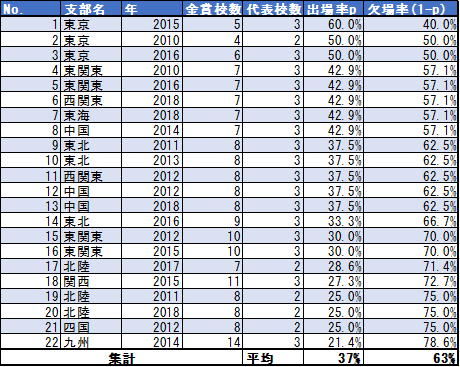
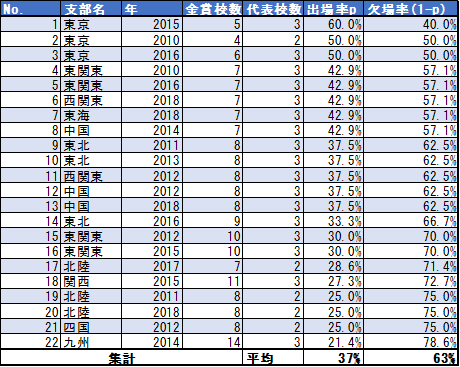
全国大会に行ける確率を調べるために、まずは『マインドスケープ』を演奏して金賞が出た22回すべての支部大会について、金賞を受賞した校数と全国への代表枠の数を調べました。
その後金賞を受賞した学校の中から同じ確率で代表が選ばれると仮定したとき、それぞれの全国出場率を各大会別に計算しました。
次に、0~22校が全国の代表に選ばれる確率を、この出場率がバラバラの全22回の大会の中から計算しなくてはなりません。
全22回の大会の内1校も全国代表に選ばれない場合の確率は、各大会の欠場率をかけ合わせれば計算できます。
次に、1校だけ全国大会に出場する場合の確率は、No.1の大会で代表になりその他は落選した場合、No.2の大会で代表になりその他は落選した場合…と、全22通りを計算し、すべてを足し合わせることで計算できます。
さて、2校出場した回数はどう計算しましょう。2校出場した場合の確率は\({}_{22}C_{2} = 231
\)で全231通りを計算しなくてはなりません。3校の場合は \({}_{22}C_{3} = 1540\)で全1,540通り。4校は \({}_{22}C_{4} = 7315\)で全7,315通りです。
このように、計算はかなり厄介で、すべてを正確に計算しようとすると実に全4,194,304通り(\((2^{22})\)の計算が必要です。
これはさすがに手計算では無理なので、Excelのvba機能でプログラムを作り、全通りを計算しました。
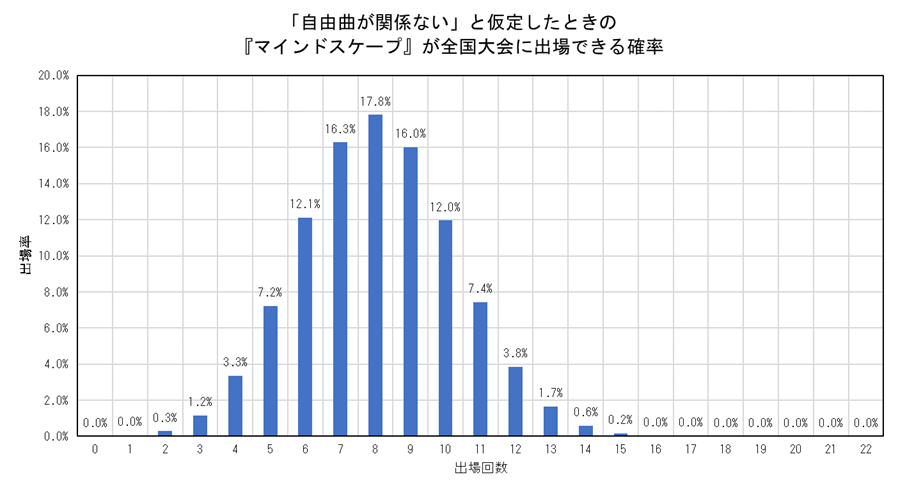
「全国出場に自由曲は関係ない」という前提では、22校中8校が全国に出場する場合が最も確率が高いようです。
出場回数で各確率を累計していくとこんな感じです。
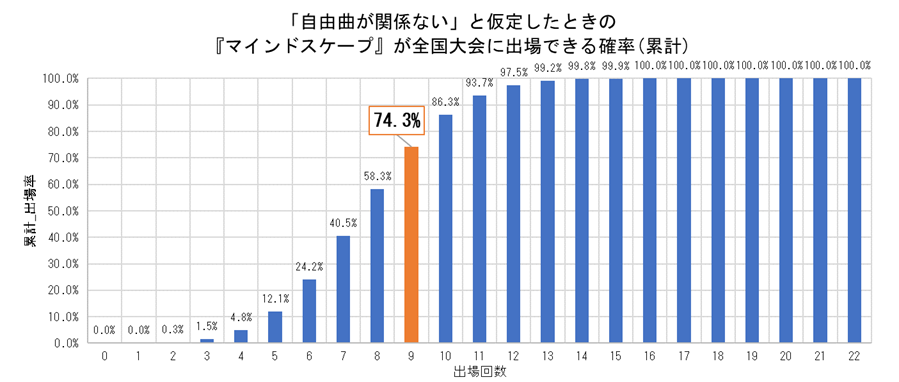
計算によると出場回数が0~9回となる確率の合計は74.3%であり、10回出場できる確率は100%- -74.3% = 25.7%より、上位25.7%であることが分かりました。
検定の結果
どうやら今回起きた「22校中10校が出場する」という現象は上位25.7%の確率で生じるようです。
これはα(上位5%)を大きく上回るため、今回の検定では「有意差なし」となります。
この結果から 「全国出場に自由曲は関係ない」 が正しいということになり、『マインドスケープ』は全国大会に行きやすい曲ではないと判断できそうです。
- 期間は直近10年分(2010~2019年度)
- すべての支部大会の中学の部を対象(中学のみを対象)
- 支部大会で『マインドスケープ』を演奏し金賞を受賞した学校がある大会のみを対象
- 「金賞を受賞した団体はすべて同じ確率で全国大会に行ける」という仮説を考える
- 仮説が正しいとしたときに、10回以上全国大会に出場できる確率が上位5%以下(α=5%)の場合、仮説を棄却し、『マインドスケープ』は統計的に「全国大会に行きやすい自由曲」と判断する。
「そうかそうか、『マインドスケープ』は全国大会に行きやすい曲ではないんだなぁ」と思ったあなた!
ちょっと待った!!!
実はまだ「『マインドスケープ』が全国に行きやすい自由曲である」という可能性は残っているのです。

本来『マインドスケープ』は全国大会に行きやすい曲だったとしても、今回たまたま少ない回数しか出場できなくて、偶然にも全国に行きやすい曲と判断できなかったという可能性があります。
ということで、『マインドスケープ』が特別全国に行きやすい曲ではないと言い切れるのかどうか、こちらも検証しました。
『マインドスケープ』は「全国大会に行きやすい自由曲ではない」と言い切れるのか
自由曲が関係ないと仮定した場合、各支部大会の全国出場率を平均すると約37%となります。
『マインドスケープ』の本来の全国出場率が37%より高い場合でも、今回の検定では「有意差なし」と判断され、『マインドスケープ』は全国大会に行きやすい曲ではないと判断されてしまう確率はどのくらいあるのでしょうか?
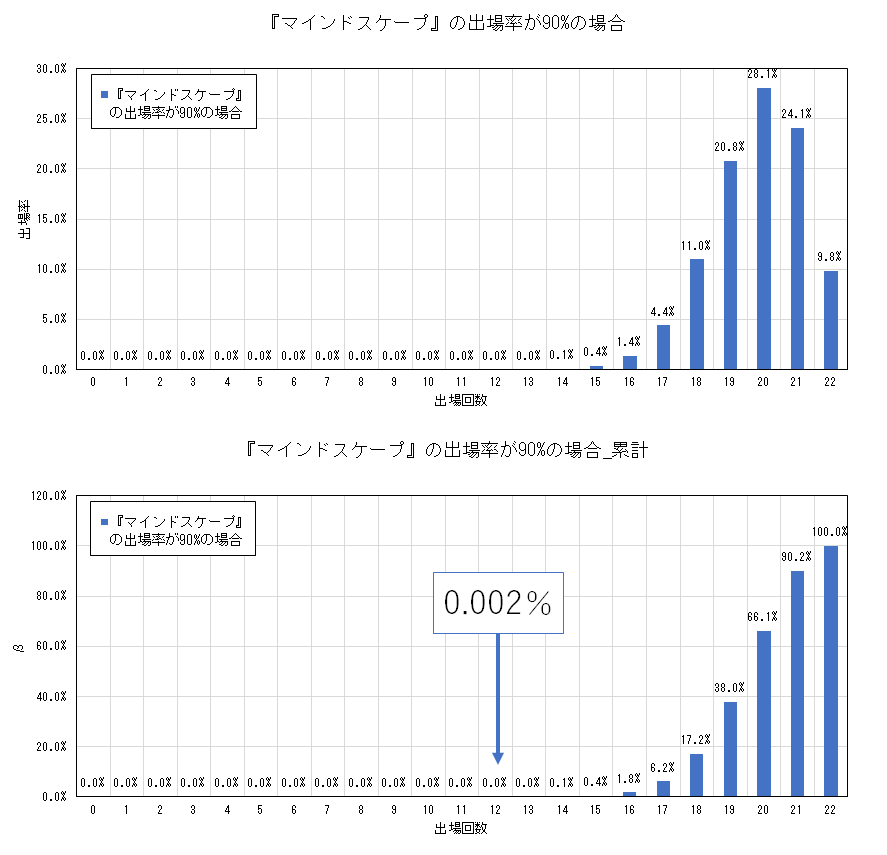
ではここで、『マインドスケープ』の全国出場率をある数値(P)と仮定したとき、今回の検定で「有意差なし」となってしまう確率(ここではβと表記する)を見ていきましょう。
先ほどの検定では22校中12校以下しか全国に行かなった場合、その確率は100%-93.7%= 6.3%となり、5%より大きいので「有意差なし」と判断されてしまいます。
よって、本来の出場率をある値に仮定したときの22校中12校以下しか全国に行かない確率を計算すれば、今回の検定で「有意差なし」と判断される確率を求めることができます。
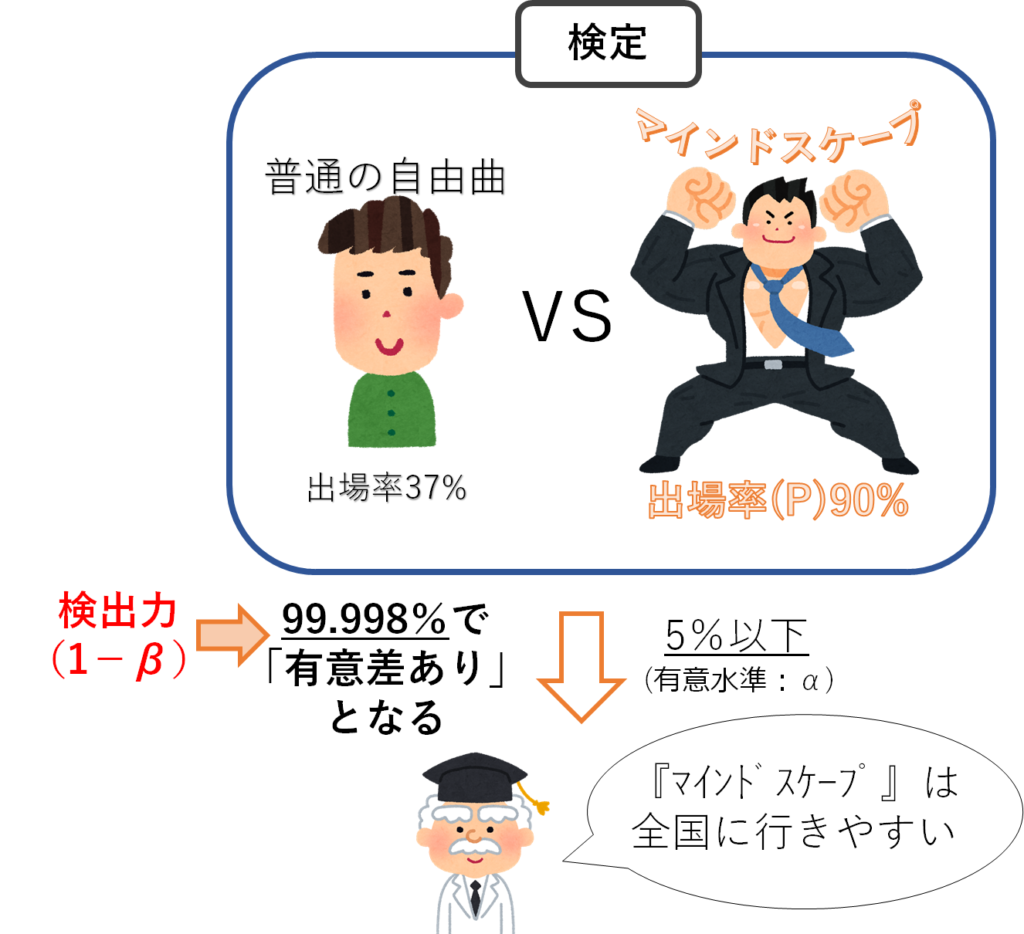
『マインドスケープ』を演奏したら本来は90%の確率で全国に行けると仮定した場合、出場校が12以下となる確率βは以下の式で計算できて0.002%となります。
$$ \small{β = \sum_{k=0}^{12} \{ {}_{22}C_{k}0.9^k(1-0.9)^{22-k} \} = 0.002\%} $$
この場合は逆に、99.998%の確率で13校以上が全国に行くため、検定を行えばほぼ確実に「有意差あり」と判定できることが分かります。
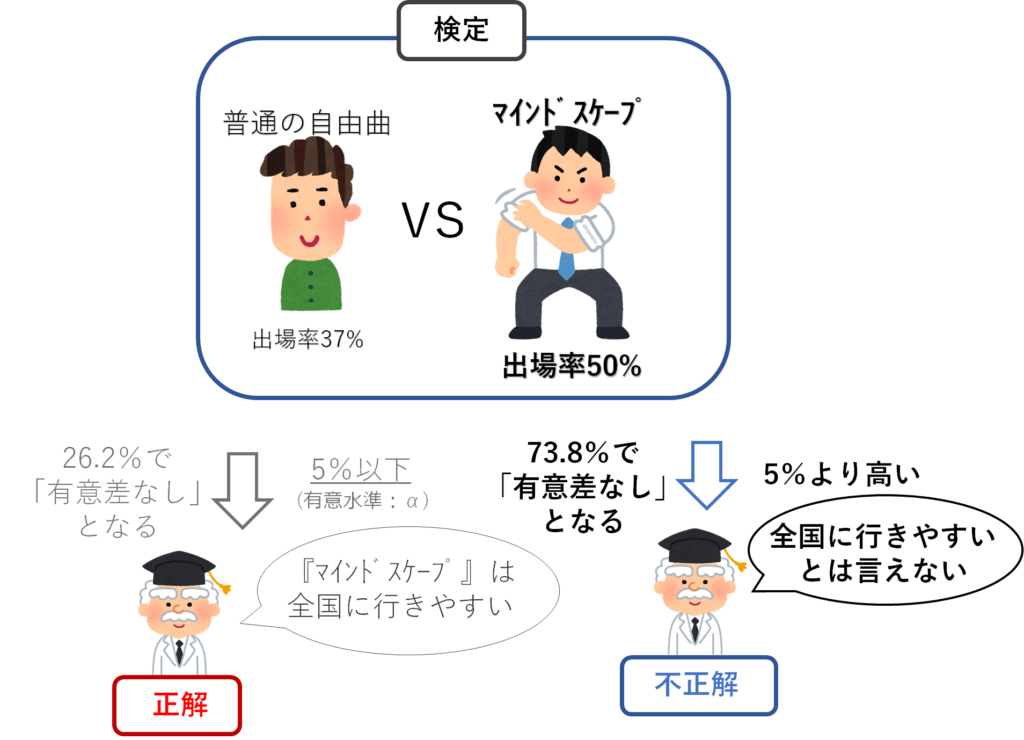
次に、今度は数値を変えて『マインドスケープ』を演奏したら本来は50%の確率で全国大会に行けるとします。(平均の全国出場率は37%なのでそれよりは高い)
この場合は以下の式で計算できて、、出場校が12校以下となる確率βは73.8%もあります。
$$ \smallβ = \small{\sum_{k=0}^{12} }\small{\{ {}_{22}C_{k} }\small{(\frac12)^{22}} \} = \small{73.8}\small{\%} $$
本当の出場率が50%で平均(37%)より高いとしても、今回の検証では73.8%もの確率で「有意差なし」となってしまいます。逆に13校以上が出場して「有意差あり」と判定される確率は26.2%しかありません。
つまりこの場合、検定を行っても間違っている確率の方が高く、この検定はあまり信用できないということになります。
このように、本来の『マインドスケープ』の全国出場率が37%に近くなればなるほど、本当は出場率が高いのに、検定の結果では「有意差なし」となる確率が高くなり、検定の結果を信用できなくなってきます。
今回の検定では「有意差なし」という結果が出いていますが、『マインドスケープ』の本来の出場率によって、この結果を信じるのか、信じないのか決めた方がよさそうです。
そうなると、「じゃあ『マインドスケープ』の全国出場率が何%の時は今回の結果信用していいの??」という疑問が生じてきますよね。
『マインドスケープ』の全国出場率がどのくらいあれば、今回の結果を信用できるのか?
検定が正しいのかどうかを示すパラメーターとして検出力というものがあります。
検出力は1-βで計算でき、検定の結果が正しい確率を示す数値です。
全国出場率を90%とした場合、22校中12校以下となる確率βは0.002%しかないので、検出力1-βは99.998%です。これだけ高い確率であれば検定の結果を信用してよさそうです。
次に、全国出場率を50%と仮定したとき、22校中12校以下となる確率βは73.8%であり、検出力1-βは 26.2%です。検定の結果が正しい確率が3割程度しかないので、この場合は検定の結果は信用できません。
では、検定の結果を信用するには検出力(1-β)をどのくらいで線引きすればよいのでしょうか?
検出力(1-β) の線引きに厳格な決まりはなく、ケースバイケースで自由に設定していいのですが、統計の世界では検出力(1-β)が80%以上のときに、その検定を信用する場合が多いです。
ということで今回も検出力(1-β)が80%以上の場合に検定を信用することとしましょう。
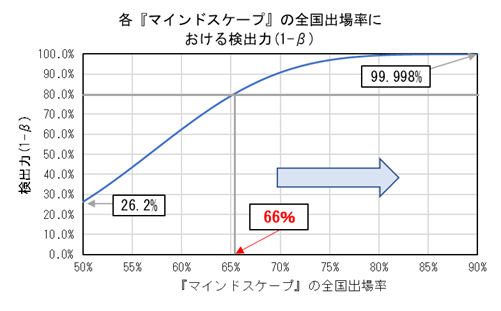
『マインドスケープ』の全国出場率と検出力(1-β)の確率の関係を計算すると以下のようになります。
計算の結果、『マインドスケープ』の全国出場率が66%以上の時は(1-β)が80%を超えることが分かりました。
このことから『マインドスケープ』の全国出場率が66%以上の場合は、今回の検定を信用してよいと言うことが分かりました。
例えば、あなたが全国出場率が70%であるような高確率で全国大会に出場できる自由曲を探している場合は、『マインドスケープ』は選ぶべきではない曲であると、今回の結果からはっきり述べることができます。
ちなみに、本来の出場率が37%~66%の間のどこにあるかを調べるには、データの数をさらに増やす必要があります。
たとえば『マインドスケープ』の出場率が50%より高い場合に、検出力を80%以上で検出したければ最低90校分のデータが必要です。今回は10年で22校分でしたから、追加で40年分程度のデータが集まれば分かるかもしれません。

ちなみに『マインドスケープ』の作曲は2005年なので、今回より多くのデータを集めることはできません。悲しいですね。
どの確率の場合にどのくらいデータ数が必要であるのかについては、説明がさらに長くなるので解説はまた別の機会に。
結論_ 『マインドスケープ』は全国大会に行きやすい曲と言えるのか
長ったらしく分析しましたが、いよいよこの小題の結論です。
『マインドスケープ』は全国大会に行きやすい曲と言えるのか?
最終的な答えは「全国出場率66%以上の能力では、全国大会に行きやすい曲とは言えない。」となります。

全国出場率が66%より低い領域で有意に全国大会に行きやすいかどうかは不明です。調べるためにはデータの数が足りません。
- すべての支部大会の中学の部を対象(中学のみを対象)
- 支部大会で10回以上金賞を受賞したデータのみを対象(データ数確保と実力による差を無視するため)
- 『マインドスケープ』を演奏した大会のみを対象
- 「金賞を受賞した団体はすべて同じ確率で全国大会に行ける」という仮説を考える
- 仮説が正しいとしたときに、10回以上全国大会に出場できる確率が上位5%以下(α≦5%)の場合、仮説を棄却し、『マインドスケープ』は統計的に「全国大会に行きやすい自由曲」と判断する。
- 検出力(1-β)は80%以上とした。(β≦20%とした。)
全国大会に行きやすい曲の見つけ方
ここまで分析しておいて最終的な結論が「『マインドスケープ』が全国に出場しやすい曲かどうかはわからない」だけではさすがに骨折り損です。
ということで、『マインドスケープ』で使った分析手法をもとに、「全国大会に行きやすい曲」がないか探してみることにしました。
全国出場率の近似について
各曲の分析を行うにはすべての曲について以下の3ステップを行わないといけません。
『マインドスケープ』の時もそうでしたが、各曲が演奏された支部大会はそれぞれで金賞の数と代表の枠が異なり、いちいち全通り計算しないと正しい全国出場率を算出することができないのです。
この複雑な計算を全曲に対して行うのはさすがに大変なので、なにか簡単に計算できる方法が必要です。
そこで、全国大会に行ける確率を平均して、「どの支部大会でも一律〇%で全国大会に行ける」とで近似すれば、その計算は二項分布ですぐに計算することができます。
先ほど計算した『マインドスケープ』の場合、すべての全国出場率を平均すると37%でした。
ここで、すべての支部大会で1回あたり一律37%で全国大会に行けると仮定します。n校が出場できる確率を\(P_n\)とすると、以下の式で計算が可能です。
$$ P_n = {}_{22}C_{n}0.37^n(1-0.37)^{22-n}\\\ ただしnは整数かつ 0≦n≦22$$
上記の式を計算した結果と、全通り計算した結果と比較すると以下のようになります。(オレンジが2項分布、青が全通り計算したものです。)
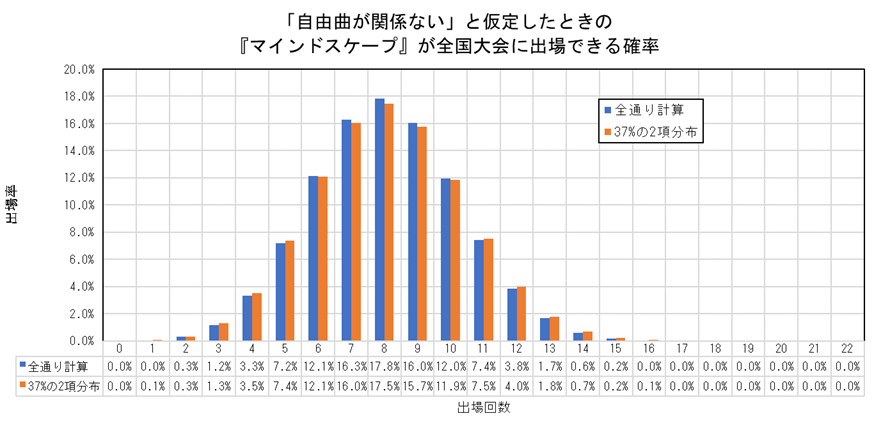
非常に形が似ていますね。
累計の確率についても22校中9校が全国大会に行く確率は73.9%で、全通り計算した74.3%と比べて申し分ないくらいに近い値で近似できていることが分かります。
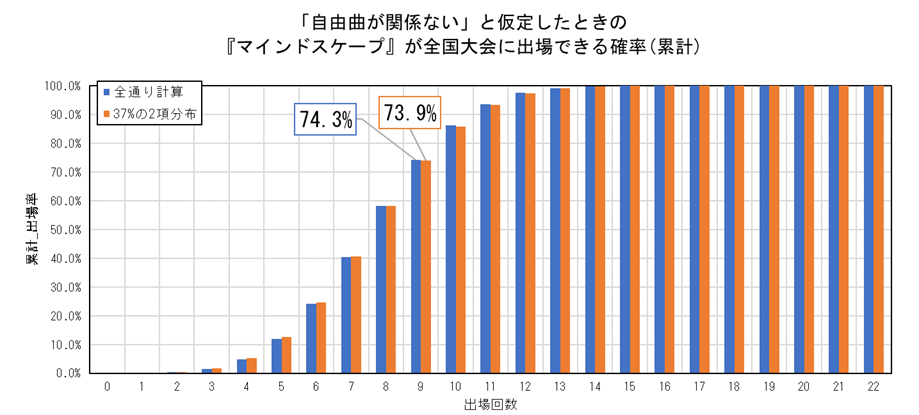
ということで、今後は全国大会に出場できる確率はその曲が演奏された支部大会の全国出場率を平均したもので代表することにします。
これにより、瞬時に全国に行ける確率を各回数ごとで計算することができるようになりました。
ではさそおく、支部大会の金賞回数が10回以下の自由曲も含めてすべて検定にかけていきましょーー!と言いたいのですが、、、
ここで注意が一点、この計算で求められる確率はあくまで近似値なので、実際の値より少しずれが予想されます。よって、優位水準αを0.10として少し緩めに検定をかけたいと思います。
「有意差なし」となった曲について
今回の検定で「有意差なし」となった曲については、本当に「全国大会に行きやすい曲と言えないのか」判断するため、検出力も計算しました。
ここでは本来の全国出場率を67%と仮定して、検出率が80%以上となったものについてのみ、「全国大会に行きやすいとは言えない曲」としています。
検出率が80%を下回っているものについては「データ不足」とし、結論を避けました。
統計的に「全国大会に行きやすい曲」と判断された6曲
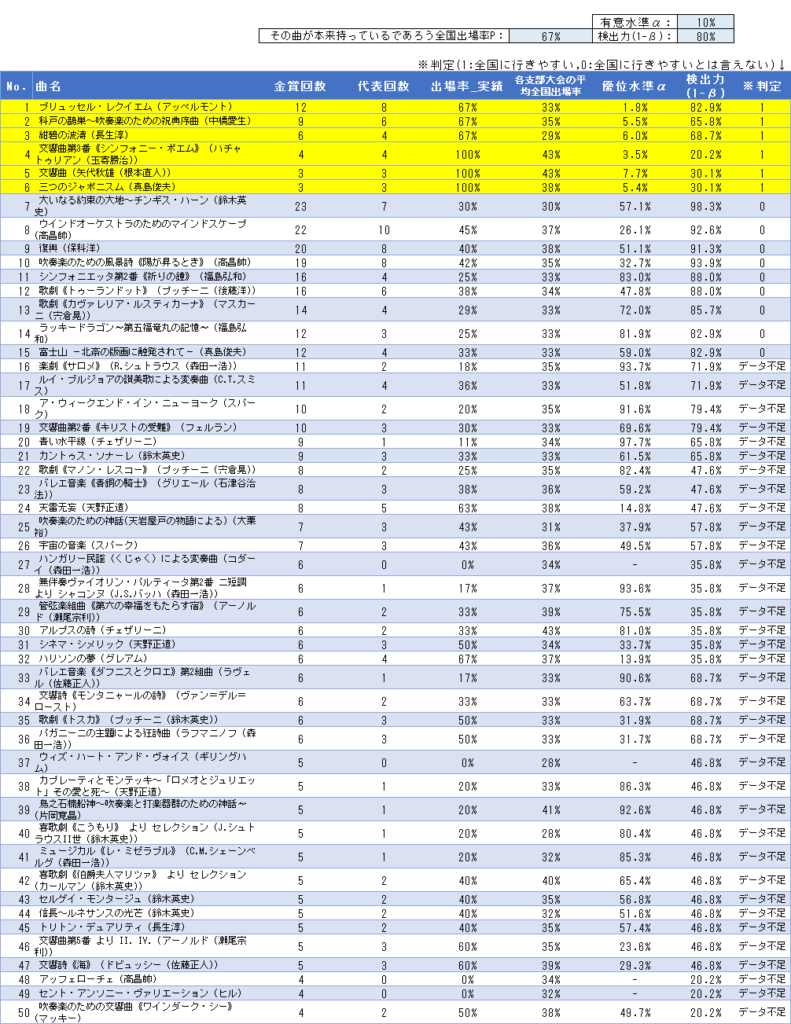
2010年~2019年の支部大会で金賞を受賞した自由曲375曲すべてを検定にかけました。
検定の結果、「全国大会に行きやすい曲」と判断された自由曲は、
なんと6曲もありました!!!
- 期間は直近10年分(2010~2019年度)
- すべての支部大会の中学の部を対象(中学のみを対象)
- 支部大会で金賞を受賞したデータすべてを対象(実力による差を無視するため)
- 「金賞を受賞した団体はすべて同じ確率で全国大会に行ける」という仮説を考える
- 1回の支部大会で全国に行ける確率は、その曲が演奏されたすべての支部大会の全国出場率の平均値とする。
- 仮説が正しいとしたときに、実績の回数以上に全国大会に出場できる確率が10%以下(α≦0.10)の場合、仮説を棄却し、その曲は統計的に「全国大会に行きやすい自由曲」と判断する。
- 本来その曲が持っている全国出場率を67%と仮定し、検出力(1-β)が80%に満たないものついては「データ不足」とし結論を見送った。
上記の意味が分からん!という人は↑で説明しているのでこちらからどうぞ。 全国大会に行きやすい曲の調査
せっかくなので各曲を紹介していきましょう。名曲ぞろいです。
ブリュッセル・レクイエム(アッペルモント)
ベルギー出身の人気作曲家、ベルト・アッペルモント(1973~)の作品です。
2016年3月22日に彼の出身国、ベルギーの首都「ブリュッセル」で起きた連続爆破テロの犠牲者に思いを馳せ、レイクエムとして作曲されました。
テロによる恐怖、怒り、悲しみなど様々な感情、また世界の平和を願う力強い作品です。この曲は、もともと英国式ブラスバンド(金管バンド)のために書かれた曲ですが、作曲家自身が吹奏楽版に編曲しています。
楽譜は¥49,093(税込)です。

科戸の鵲巣~吹奏楽のための祝典序曲 (中橋愛生)
陸上自衛隊中央音楽隊の委嘱作品として2004年に中橋愛生が作曲したものです。
タイトルの読み方は「科戸の鵲巣」(しなとのじゃくそう)です。
タイトルの意味と解説が楽譜の販売ページに載っていましたので一部引用したいと思います。
「科戸の風」(しなとのかぜ)という言葉がある。これは「一切の穢れを吹き去ってくれる風」のこと。「科戸」単独では「風の起こる場所」の意である。また、「鵠巣(じゃくそう)は風の起こる所を知る」という諺がある。カササギにはその年の風の具合を予見して巣を作る本能があると言われており、「未来を予知する能力」を例えている。この二つの言葉を合成し、「風の起こる場」である吹奏楽のための、祝福された未来へ向かう序曲のタイトルとした。
未来は過去や現在の行き着く先にあり、それらを包括したものが《歴史》である。「異なった時空」である幾つかの音響や動機が様々に「重なり合う」ほか、時には同一の旋律さえも重層的に響き合う。そうした「時の積み重ね」の行き着く先に、それまでに潜在的に堆積してきたものが前面に顕われるのである。
この曲は、公的には初演が最後の定例演奏会となられて退官された音楽隊の野中図洋和・元隊長、私的には初演の頃に結婚をされた大切な友人、というお二人の新しい門出に捧げられている。祝典曲として、普段の私のスタイルとは少々違う引き出しを開けたものとなった。
https://www.brain-shop.net/shop/g/gYDON-C02/?item=refer
「鵠巣(じゃくそう)は風の起こる所を知る」っていう諺はこの曲の解説でしか聞いたことがなく、中橋愛生の知識の多さに感服します。
ちなみに「鵠」は(こく)と読み、白鳥を指す感じです。この曲では代わりにカササギを意味する「鵲」を使うことで「祝福された未来へ向かう」という意味を表しているのですね。
楽譜はコンクール用にカットしているものが出版されており、価格は¥33,000(税込)です。

紺碧の波濤 (長生淳)
「紺碧」(こんぺき)はやや黒みを帯びた青い色のことで、「波濤」(はとう)は「大きな波」という意味です。その意味合いから、寒そう、冷たそう…という印象が喚起されます。
作曲者による曲の解説を見つけましたのでご紹介します。
この曲は「悲劇の英雄」をテーマにした創価グロリア吹奏楽団の委嘱作品。これは誰しも思い描くものがそう変わらないもののようでいて、しかし案外人によって、誰を思い浮かべるかが違うのではないでしょうか。どういうところに英雄らしさを感じるか。それが、結構違うからなのだと思います。私は、どの人というのではありませんが、悲劇の中にあって、運命をうらむのではなく静かに受け入れる、そんな人物に憧れを感じます。それは諦めとは違い、背筋がすっと伸びた生き方で、凛とした気概、と言ってもいいかもしれません。そんな英雄が、暗い波濤に滅びの予感を重ねて見据え、静かに受け入れつつも、さすがに胸の内には様々な思いが去来する・・・といったところを描いたのが曲の前半で、後半では、その波濤の真っただ中に入っていきます。(長生 淳)
http://www.cafua.com/products/detail576.html
「悲劇の英雄」とはなかなか男心をくすぐるテーマですね。そしてそれに見合うほど曲がカッコいい!!中学生男子がこれを演奏していると思うと胸が熱くなる一曲です。
楽譜は39,050 円(税込)です。
交響曲第3番《シンフォニー・ポエム》 (ハチャトゥリアン (玉寄勝治))
検定で見事「全国大会に行きやすい曲」という結果になったこの曲ですが、なんと、演奏しているのは羽村第一中学校ただ1校だけです。
そして編曲者の玉寄勝治さんは羽村第一中学校吹奏楽部の顧問の先生です。自由曲を自給自足して全国大会に行き、しかもその確率が高いというバケモノです。
ちなみに玉寄勝治さんはブログもやっているようですよ。こちら
この曲は羽村第一中学校吹奏楽部の専売特許になっているため楽譜の出版はありません。どうしても欲しいという方はブログから玉寄勝治さんに直談判するしかないでしょう。
交響曲 (矢代秋雄 (根本直人))
矢代秋雄(やしろ あきお)(1929年9月10日 – 1976年4月9日)は1940~1960年頃にかけて活躍した日本人作曲家です。当時では珍しく、西洋音楽に非常に長けている人でした。
この曲は日本フィルハーモニー交響楽団が日本の作曲家に対する作品委嘱シリーズの第1作として、1956年にパリ留学を終えて帰国した矢代秋雄に委嘱したもので、矢代が敬愛するセザール・フランクの交響曲を念頭に置いて書かれた作品です。
クライマックス(6:53~)が非常にドラマティックで、とってもカッコいい一曲です。
楽譜は¥55,000円(税込)です。

三つのジャポニスム (真島俊夫)
この曲は東京佼成ウインド・オーケストラの委嘱により作曲されました。日本的な題材を西洋的な技法で表現しています。
「ジャポニスム」というのは19世紀に欧米の芸術界で流行した「日本趣味」のことで、浮世絵からインスピレーションを受けたゴッホや、プッチーニの「蝶々夫人」が有名です。
「日本の音楽文化を西洋音楽の技法で再現する」というまさに「ジャポニズム」な1曲です。
全曲演奏すると約16分40秒もある大作ですが、コンクール用に約7分30秒にアレンジしたコンポーザーズ・エディションが出版されています。楽譜は¥47,300(税込)です。

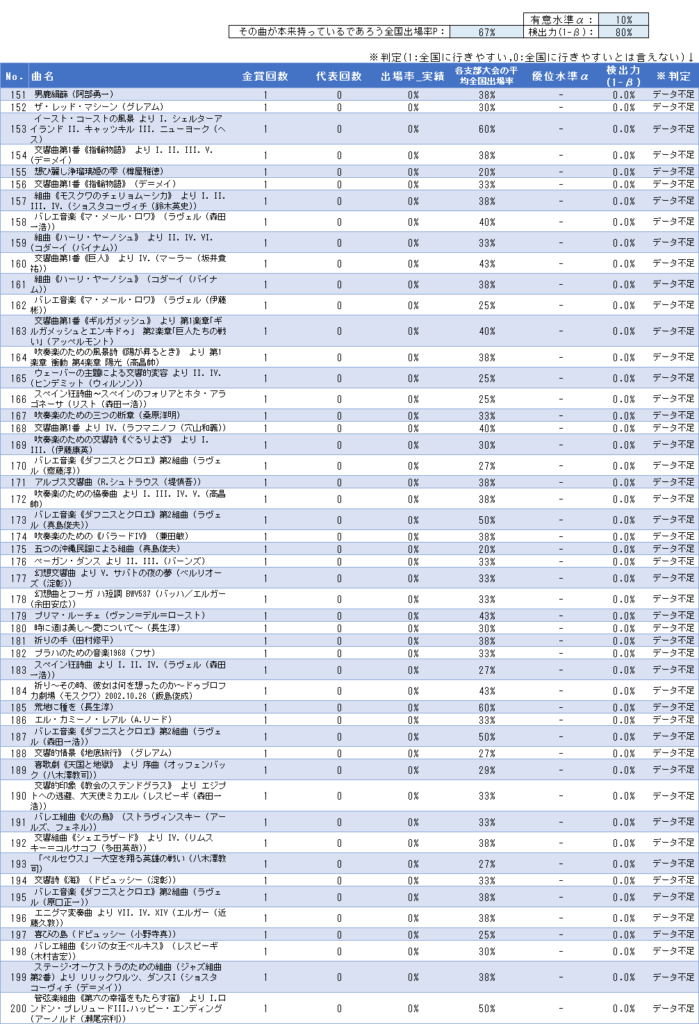
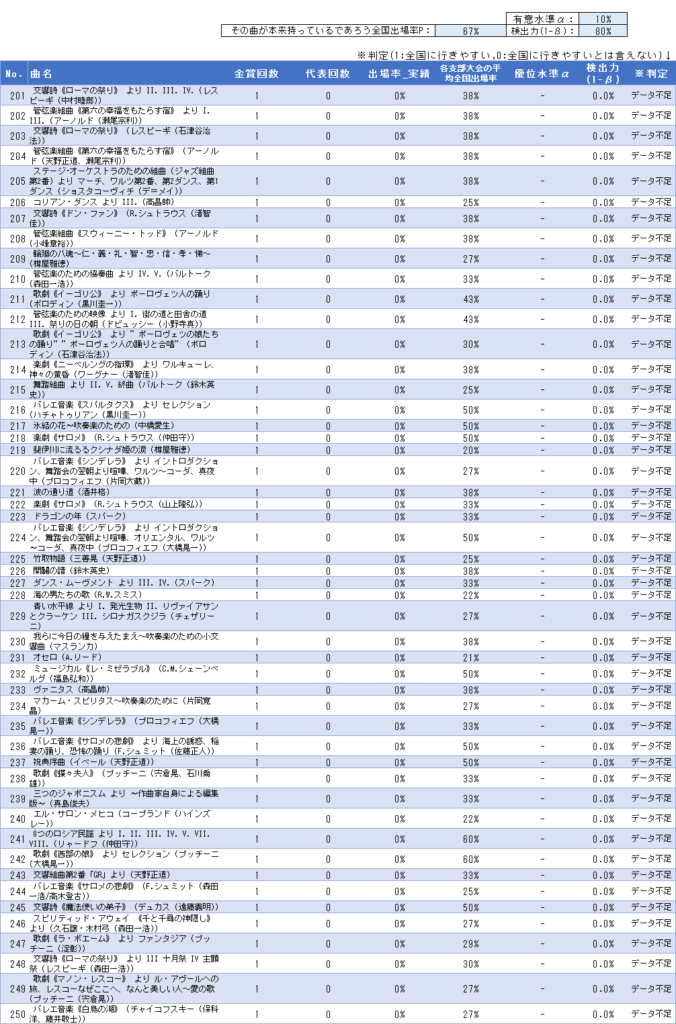
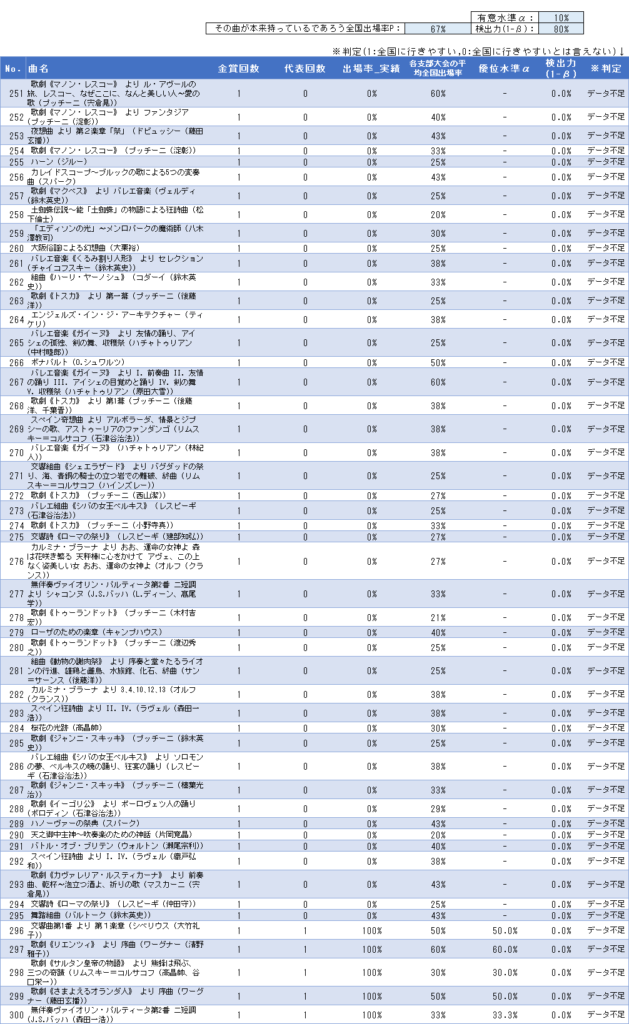
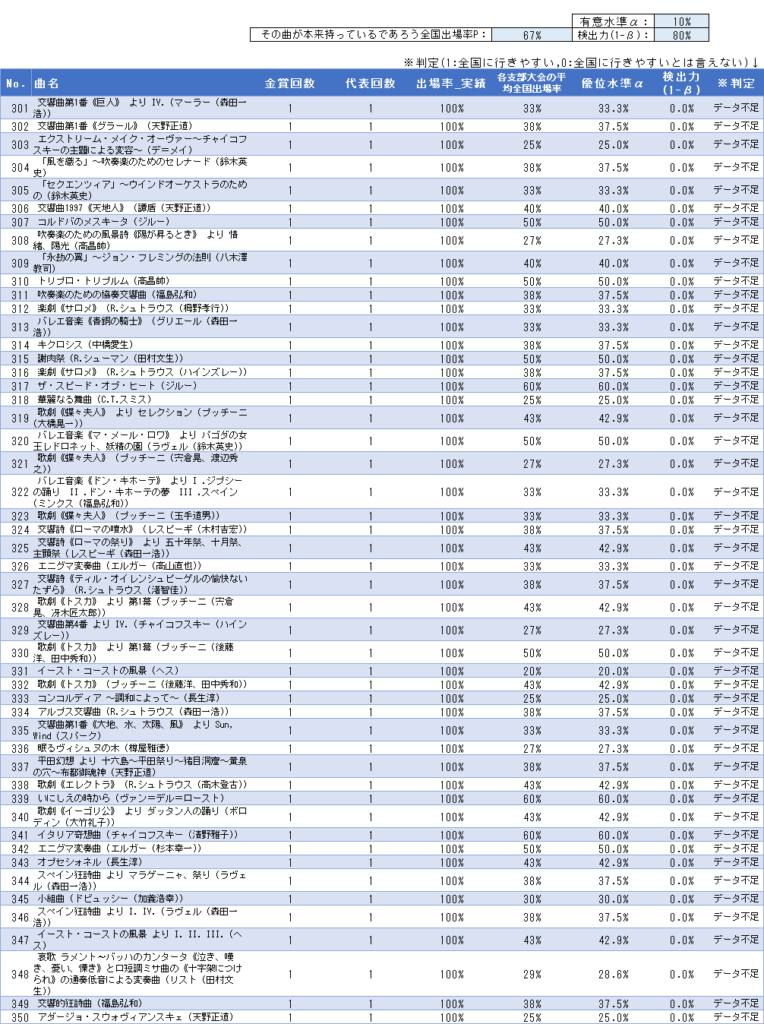
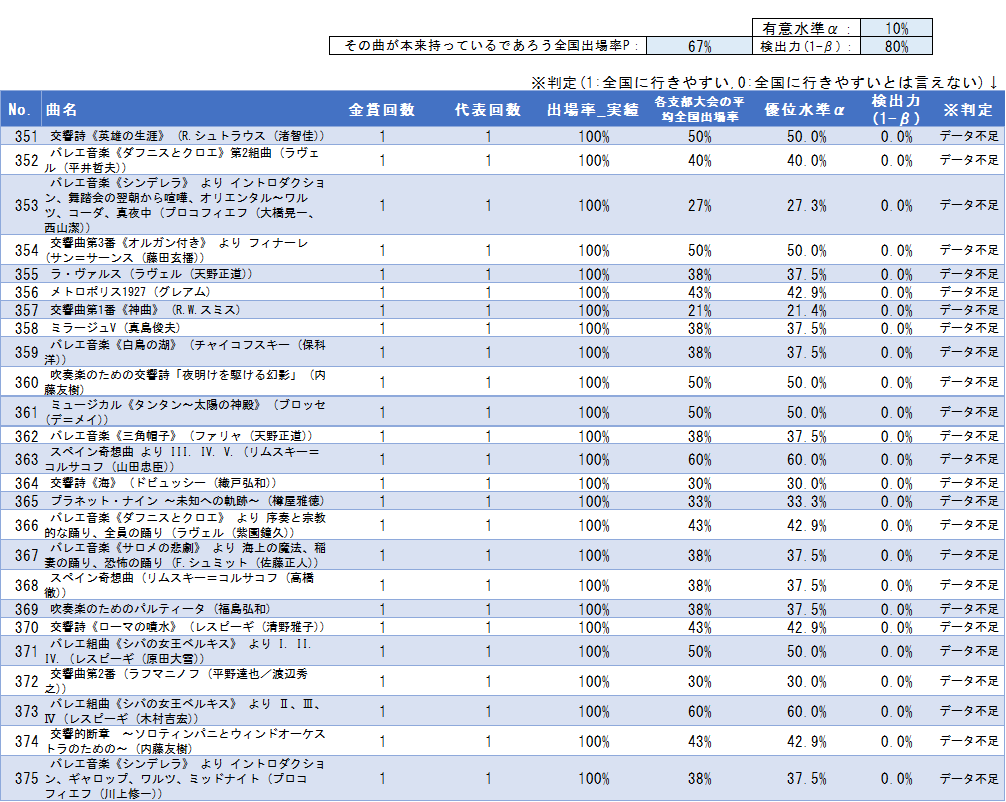
全375曲の検定結果一覧
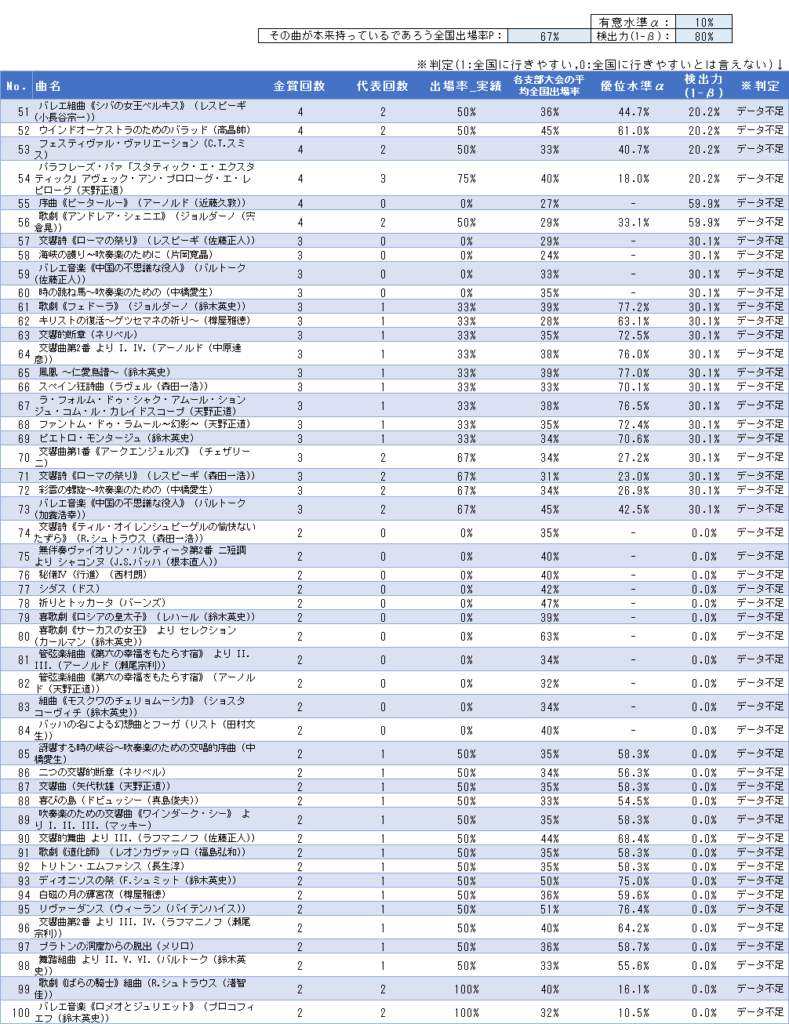
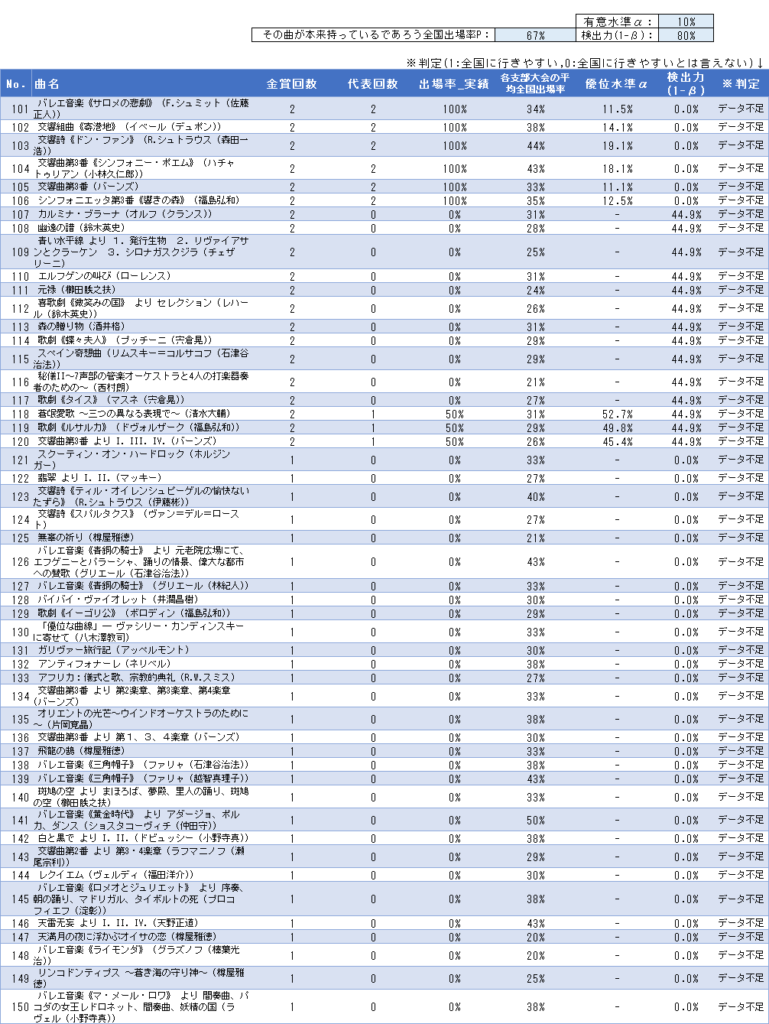
その他「有意差なし」となった曲も合わせて、375曲すべての検定結果は以下の通りです。自由曲選びの参考にしてください。
使いやすいようにエクセルファイルも配布します。こちらからダウンロードください。全375曲のエクセルデータ
まとめ_データの配布
今回は過去の吹奏楽コンクールの結果を統計的に分析し、全国大会に行きやすい自由曲があるのか調査しました。
調査の結果、以下の6曲が全国に行きやすい自由曲ということが分かりました。全部の結果を見たい人はこちらからエクセルファイルをダウンロードしてご確認ください。
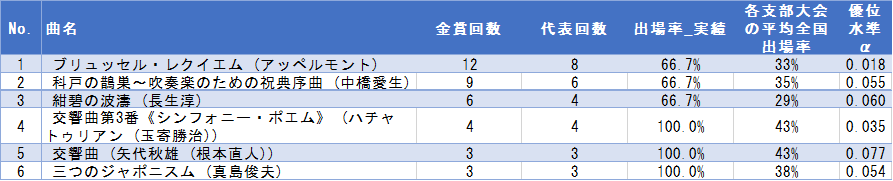
- 期間は直近10年分(2010~2019年度)
- すべての支部大会の中学の部を対象(中学のみを対象)
- 支部大会で金賞を受賞したデータすべてを対象(実力による差を無視するため)
- 「金賞を受賞した団体はすべて同じ確率で全国大会に行ける」という仮説を考える
- 1回の支部大会で全国に行ける確率は、その曲が演奏されたすべての支部大会の全国出場率の平均値とする。
- 仮説が正しいとしたときに、実績の回数以上に全国大会に出場できる確率が10%以下(α≦0.10)の場合、仮説を棄却し、その曲は統計的に「全国大会に行きやすい自由曲」と判断する。
- 本来その曲が持っている全国出場率を67%と仮定し、検出力(1-β)が80%に満たないものついては「データ不足」とし結論を見送った。
この6曲を演奏して、支部大会で金賞を受賞すれば、全国大会に選ばれる確率は高そうです。
しかし、今回の分析はあくまで「支部大会→全国大会」の選考で有利というだけで、地区大会→県大会、県大会→支部大会の道のりをこの曲で乗り越えられるかどうかは考慮していません。
今回ピックアップされた6曲はどれも演奏の難易度が恐ろしく高いですが、各大会で勝ち抜くに行くにはこれらの曲を高い完成度で演奏しなければなりません。
その練習は必然的に過酷で、1人が頑張ればどうにかなるというものでもないです。団員みんなが文字通り一致団結し、本気で練習してやっと、全国大会の切符を手に入れるチャンスが得られるということです。
コンクールでいい成績を残したいのなら、こんな難しい曲を選ぶより、自分たちの実力を思う存分発揮できる難易度の自由曲にした方がいいのかもしれません。
本気で全国大会を目指すのであれば、地区大会での落選も覚悟で、この高難易度の曲を吹きこなすことができるまでの長く苦しい練習を乗り越える覚悟が必要です。
今回データを分析して私が感じたのは「自由曲を何にしても全国大会の壁は大きく、乗り越えるのは大変だな」ということでした。
ここまでお読みいただきありがとうございました。
分析の内容についての質問や、他にもこういうことを分析してほしい等、要望がありましたらぜひコメント欄までよろしくお願いいたします。










コメント